约定下标从 1 开始。
字符串匹配问题
给定字符串 s1,以及模式串 s2,求 s2 在 s1 内的所有出现位置。
一个很朴素的想法就是一位一位进行比较,复杂度 O(MN),M,N 为两字符串长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| const int N = 1e6+5;
char s1[N],s2[N];
void brute_force(){
int l1 = strlen(s1);
int l2 = strlen(s2);
for(int i=0;i+l2<=l1;i++){
bool flag=1;
for(int j=0;j<l2;j++){
if(s1[i+j]!=s2[j]){
flag=0;break;
}
}
if(flag)printf("match at %d\n",i);
}
}
|
KMP 算法
然而,KMP 算法可以让我们在 O(M+N) 的时间复杂度内求出所有出现位置。(算法名字来源于三个发明者的姓名首字母)
其核心思想就是减少不必要的比较操作(一位一位跳太慢了,有时候我们可以比较了之后就一次跳好多位)
next 数组
next 数组代表一个下标失配后,可以直接跳过多少个字符。
next[i] 的定义为,模式串 s2 的前缀 [1…i] 中,相同的真前缀和真后缀最大长度。
来看一个例子:
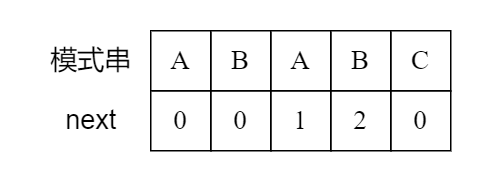
那么这个 next 数组到底怎么用呢?
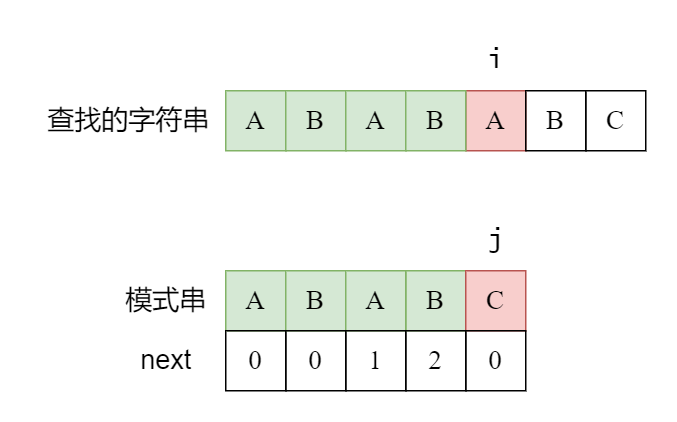
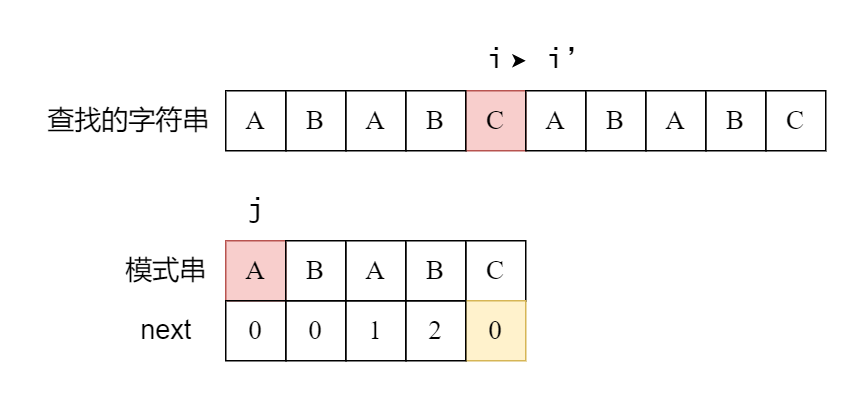
我们用两个指针 i,j,分别代表目前在查找的字符串和模式串里面的匹配位置。考虑现在匹配到 ABABA,最后一位的 A 失配。
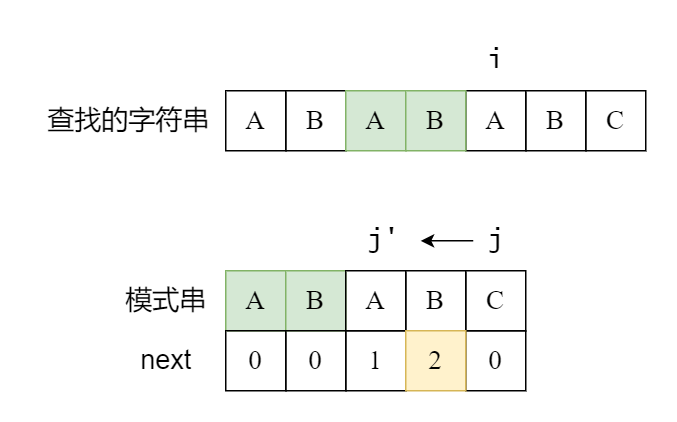
接下来发生了什么事情呢?
i 的位置保持不变j 的位置跳转到最后一位匹配的对应 next 值后一个位置(2+1=3)
这是什么意思呢?其实 ABAB 的最长相同的真前缀和真后缀长度是 2,即 AB 和 AB,这就代表我们现在匹配成功的 ABAB,其实最后两个字符已经是匹配好的下一个的开头了(而且最长就是 2,所以说一定是用重复的 AB)。所以我们已经匹配好了最后的两个 AB,而 j 的位置就跳到了匹配完 AB 的下一个,继续进行匹配。
再看一个例子:
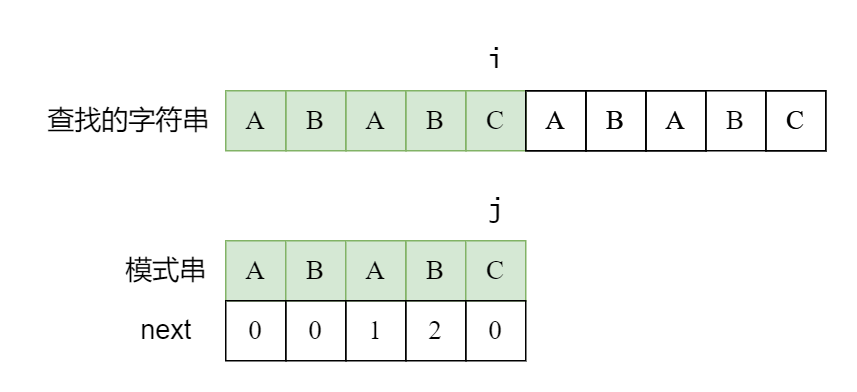
如果第一个字符就失配了,我们直接将 i 后移一位。
综上我们可以写出代码。
1
2
3
4
5
6
7
8
9
| void kmp(){
for(int i=1,j=0;i<=n;i++){
while(j && t[j+1]!=s[i])j=nxt[j];
if(t[j+1] == s[i])j++;
if(j==m)cout<<i-m+1<<'\n';
}
}
|
看到这里,有的小朋友就要问了:我看这里的 j 不是会往回跳吗?那万一疯狂往回跳,复杂度不就变成 O(nm) 了吗?
事实上,如果仔细想一想,就能发现,j 每往回跳一次,就至少匹配一次(只有匹配的时候 j 增加了),最多匹配 n 次,那么最多往回跳 n 次。
因此,匹配的复杂度是 Θ(n) 的。
求解 next 数组
接下来就只需要求出 next 数组了。
考虑从前一位的 next 数组递推。由于前一位的 next 数组已经保证了 [0..nxt[i-1]],[i-nxt[i-1]...i-1] 是相同的。
-
s[nxt[i-1]+1] = s[i]
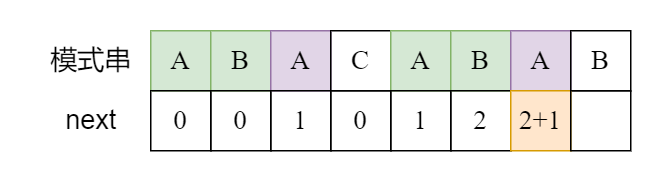
如图,显然 nxt[i] = nxt[i-1]+1。
-
s[nxt[i-1]+1] != s[i]

我们尝试退而求其次,找一个比较短的部分公共前缀部分进行匹配。而其的最长的就是紫色这里的 nxt 数值,因此我们将已经匹配的长度减小到 1,然后再看是否可以匹配。(注意,这里的找一个比较短的部分的过程可以进行多次)
1
2
3
4
5
6
7
8
| void cal_next(){
for(int i=2,j=0;i<=m;i++){
while(j && t[j+1]!=t[i])j=nxt[j];
if(t[j+1]==t[i])j++;
nxt[i]=j;
}
}
|
如何说明复杂度?观察 j,不难发现 j 最多只会增加 m 次,所以也最多只会往回跳 m 次。
完整代码
[洛谷P3375] 【模板】KMP 字符串匹配
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<bits/stdc++.h>
using namespace std;
const int N = 1e6+6;
char s[N],t[N];
int nxt[N];
int main(){
ios::sync_with_stdio(0);cin.tie(0);
cin>>(s+1)>>(t+1);
int n=strlen(s+1),m=strlen(t+1);
for(int i=2,j=0;i<=m;i++){
while(j && t[j+1]!=t[i])j=nxt[j];
if(t[j+1]==t[i])j++;
nxt[i]=j;
}
for(int i=1,j=0;i<=n;i++){
while(j && t[j+1]!=s[i])j=nxt[j];
if(t[j+1] == s[i])j++;
if(j==m)cout<<i-m+1<<'\n';
}
for(int i=1;i<=m;i++)cout<<nxt[i]<<' ';
cout<<'\n';
return 0;
}
|
运用 KMP 算法解决(真)循环节问题
定义
我们称字符串 s 有长度为 x (x<∣s∣) 的循环节 s[1..x],当且仅当 ∀1≤i≤∣s∣−x,都有 s[i]=s[i+x]。
我们称字符串 s 有长度为 x (x<∣s∣) 的真循环节 s[1..x],当且仅当存在长度为 x 的字符串 t 与正整数 k,使得 s 是由 k 个 t 拼接而成的。
特别地,定义 s 总是字符串 s 的循环节和真循环节。
做法
接上文,nxti 表示 s[1..i] 最长的相同的真前缀和真后缀最大长度。
定理一:i−nxti 是字符串 s[1..i] 的最短循环节长度。
证明:(有时间补)
定理二:当 i−nxti 是 i 的因数时,字符串 s[1..i] 的最短真循环节长度就是i−nxti ,否则字符串 s[1..i] 真循环节只有 s。
证明:(有时间补)
练习
LOJ #10035. 「一本通 2.1 练习 1」Power Strings
[ARC060D] Best Representation









