例题来自《信息学奥赛一本通·提高篇》。
哈希函数
设字符串为 s = c 1 c 2 … c m s=c_1c_2\ldots c_m s = c 1 c 2 … c m f ( s ) = ( c 1 b m − 1 + c 2 b m − 2 + ⋯ + c m b 0 ) m o d M f(s)=(c_1b^{m-1}+c_2b^{m-2}+\dots+c_mb^0)\bmod M f ( s ) = ( c 1 b m − 1 + c 2 b m − 2 + ⋯ + c m b 0 ) mod M M M M b b b M M M
比如说这样:
1 2 3 4 5 6 7 8 9 const int b=114 ,M=1e9 +9 ;int h (char * str) int l = strlen (str);int res=0 ;for (int i=0 ;i<l;i++){return res;
O(1) 求子串哈希
先预处理数组 H i H_i H i s s s i i i [ l , r ] [l,r] [ l , r ] H r − H ( l − 1 ) b r − l + 1 H_r - H_{(l-1)} b^{r-l+1} H r − H ( l − 1 ) b r − l + 1 b b b 0 ∼ ∣ s ∣ 0\sim |s| 0 ∼ ∣ s ∣ O ( n ) O(n) O ( n ) O ( 1 ) O(1) O ( 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 const int N = 1e6 +5 ;const int b=114514 ,M=1e9 +9 ;char pat[N];char s[N];int h[N];int bp[N];void init () int l=strlen (s);1 ]=b;for (int i=2 ;i<=l;i++){-1 ]*b%M;0 ]=s[0 ];for (int i=1 ;i<l;i++){-1 ]*b+s[i])%M;int get_hash (int l,int r) if (l==0 )return h[r];return ((h[r]-(ll)h[l-1 ]*bp[r-l+1 ])%M+M)%M;
如上代码。注意:如果你使用的是 int 存哈希,请在做乘法时全部强制转换到 long long。如果你懒得转或者你害怕你忘记转,建议直接用 long long 存哈希。
子串查找
除了用 KMP 算法,通过上面的技巧,我们也可以用 O ( n + m ) O(n+m) O ( n + m )
LOJ #103. 子串查找
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 1e6 +5 ;const int b=114514 ,M=1e9 +9 ;char pat[N];char s[N];int h[N];int bp[N];void init () int l=strlen (s);1 ]=b;for (int i=2 ;i<=l;i++){-1 ]*b%M;0 ]=s[0 ];for (int i=1 ;i<l;i++){-1 ]*b+s[i])%M;int get_hash (int l,int r) if (l==0 )return h[r];return ((h[r]-(ll)h[l-1 ]*bp[r-l+1 ])%M+M)%M; int main () int E9 = 1e9 , E6=1e6 ;int x = (E9*E9+5 )%E6;printf ("%d\n" ,x);return 0 ;scanf ("%s" ,s);scanf ("%s" ,pat);init ();int l_pat = strlen (pat);int hash_pat=0 ;for (int i=0 ;i<l_pat;i++){int l_s = strlen (s);int ans = 0 ;for (int i=0 ;i+l_pat<=l_s;i++){if (get_hash (i,i+l_pat-1 )==hash_pat)ans++;printf ("%d\n" ,ans);return 0 ;
例题
Power Strings
LOJ #10035. 「一本通 2.1 练习 1」Power Strings
给定若干个长度小于等于 1 0 6 10^6 1 0 6 ababab 最多由 3 个 ab 拼接而成。
哈希解法
枚举字符串长度所有的约数作为循环节长度,然后再判断即可。对于循环节的判定,事实上:
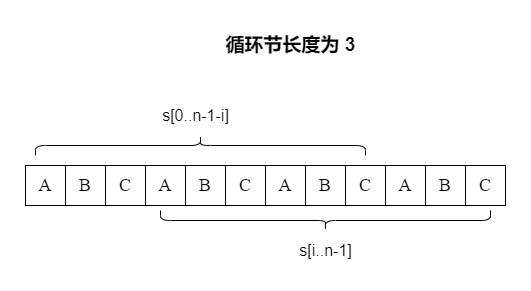
长度为 n 的字符串 s 存在长度为 i 的循环节 ⟺ s [ 0.. n − 1 − i ] = s [ i . . n − 1 ] \text{长度为 } n \text{ 的字符串 } s \text{ 存在长度为 } i \text{ 的循环节} \iff s[0..n-1-i]=s[i..n-1]
长度为 n 的字符串 s 存在长度为 i 的循环节 ⟺ s [ 0.. n − 1 − i ] = s [ i .. n − 1 ]
注意这是一个充要条件。证明不难,略去。(可看下图理解)
对于枚举约数,有一种复杂度为 O ( n ) O(\sqrt{n}) O ( n ) 1 ∼ n 1\sim \sqrt{n} 1 ∼ n x x x n n n n x \dfrac{n}{x} x n n n n
复杂度 O ( n ) O(\sqrt n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 1e6 +5 ;char s[N];bool ok;const ll b=114514 ,M=1e9 +7 ;ll get_hash (int l,int r) {if (l==0 )return h[r];return ((h[r]-h[l-1 ]*power_b[r-l+1 ])%M+M)%M;int main () 1 ]=b;for (int i=2 ;i<N;i++) power_b[i]=power_b[i-1 ]*b%M;while (1 ){scanf ("%s" ,s);if (s[0 ]=='.' )return 0 ;int l = strlen (s);0 ]=s[0 ];for (int i=1 ;i<l;i++)h[i]=(h[i-1 ]*b+s[i])%M;int ans = 1 ;for (int i=1 ;i<l;i++){ if (l%i!=0 )continue ; if (get_hash (0 ,l-i-1 ) == get_hash (i,l-1 ))ans=max (ans,l/i); printf ("%d\n" ,ans);return 0 ;
KMP 解法
本题还有一种做法是利用 KMP 算法的 next 数组,可以做到复杂度 O ( n ) O(n) O ( n )
具体来说,如果答案不是 1,那么 next[l-1] 一定存的是 答案-1 遍的重复子串的长度。设 x=l-next[l-1],若 x 是 l 的因数,那么 l 一定可以由 l/x 个相同子串重复连接成,否则答案就是 1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 1e6 +5 ;char s[N];int nxt[N];int main () while (1 ){scanf ("%s" ,s);if (s[0 ]=='.' )return 0 ;int l = strlen (s);int pre=0 ,i=1 ;0 ]=0 ;while (i<l){if (s[pre]==s[i]){else {if (pre==0 )nxt[i++]=0 ;else pre=nxt[pre-1 ];int x=l-nxt[l-1 ];if (l%x==0 )printf ("%d\n" ,l/x);else puts ("1" );return 0 ;
Seek the Name, Seek the Fame
LOJ #10036. 「一本通 2.1 练习 2」Seek the Name, Seek the Fame
给定若干字符串(这些字符串总长 ≤ 4 × 1 0 5 \le 4\times 10^5 ≤ 4 × 1 0 5
哈希解法
O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 4e5 +5 ;char s[N];114514 ,M=1e9 +7 ;ll get_hash (int l,int r) {if (l==0 )return h[r];return ((h[r]-h[l-1 ]*bp[r-l+1 ])%M+M)%M;int main () 1 ]=b;for (int i=2 ;i<N;i++)bp[i]=bp[i-1 ]*b%M;while (scanf ("%s" ,s)!=EOF){0 ]=s[0 ];int l = strlen (s);for (int i=1 ;i<l;i++){-1 ]*b+s[i])%M;for (int i=1 ;i<l;i++){if (get_hash (0 ,i-1 )==get_hash (l-i,l-1 ))printf ("%d " ,i); printf ("%d\n" ,l);return 0 ;
KMP 解法
这道题也可以用 KMP 算法求解,一样是用 next 数组。和线性递推求 next 数组的逻辑完全一样,从 next[l-1] 一步一步往回跳,最后倒序输出即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 4e5 +5 ;char s[N];int nxt[N];int main () while (scanf ("%s" ,s)!=EOF){int l = strlen (s);0 ]=0 ;int pre=0 ,i=1 ;while (i<l){if (s[pre]==s[i]){else {if (pre!=0 )pre=nxt[pre-1 ];else nxt[i++]=0 ;int > ans;push (l);int x = nxt[l-1 ];while (x!=0 ){ push (x);x=nxt[x-1 ];while (ans.size ()){printf ("%d " ,ans.top ());ans.pop ();puts ("" );return 0 ;
friends
LOJ #2823. 「BalticOI 2014 Day 1」三个朋友
给定一个字符串 S S S S S S T T T T T T U U U U U U S S S
如果字符串无法按照上述方法构造出来,输出 NOT POSSIBLE;
如果字符串 S S S NOT UNIQUE。
解法
无非就是要解决中间删去了一个字符的哈希问题。我们考虑在我们 O ( 1 ) O(1) O ( 1 )
设删去的位置为 x x x [ l , r ] [l,r] [ l , r ] x x x [ l , r ] [l,r] [ l , r ] x x x [ l , x − 1 ] [l,x-1] [ l , x − 1 ] [ x + 1 , r ] [x+1,r] [ x + 1 , r ]
复杂度 O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 2e6 +5 ;char s[N];const ll b=114514 ,M=1e9 +9 ;int x; ll get_hash (int l,int r) {if (l>r)return 0 ; if (l<=x&&x<=r)return (get_hash (l,x-1 )*bp[r-x]%M+get_hash (x+1 ,r))%M;if (l==0 )return h[r];return ((h[r]-h[l-1 ]*bp[r-l+1 ])%M+M)%M;int main () 0 ]=1 ;for (int i=1 ;i<N;i++)bp[i]=bp[i-1 ]*b%M;int n;scanf ("%d%s" ,&n,s);if (n%2 ==0 ){ puts ("NOT POSSIBLE" );return 0 ;0 ]=s[0 ];for (int i=1 ;i<n;i++)h[i]=(h[i-1 ]*b+s[i])%M;bool ok = 0 ;-1 ; int ans_x;for (x=0 ;x<n;x++){ int mid = n/2 ;if (x>mid)mid--;if (get_hash (0 ,mid)==get_hash (mid+1 ,n-1 )){if (ans_hash==-1 ){get_hash (0 ,mid),ans_x=x;1 ;else if (ans_hash!=get_hash (0 ,mid)){ puts ("NOT UNIQUE" );return 0 ;if (ok){int mid = n/2 ;if (ans_x>mid)mid--;for (int i=0 ;i<=mid;i++){if (i==ans_x)continue ;putchar (s[i]);else {puts ("NOT POSSIBLE" );return 0 ;
A Horrible Poem
给出一个由小写英文字母组成的字符串 S S S q q q S S S 1 ≤ a ≤ b ≤ n ≤ 5 × 1 0 5 1 \le a \le b \le n \le {5\times 10^5} 1 ≤ a ≤ b ≤ n ≤ 5 × 1 0 5 q ≤ 2 × 1 0 6 q \le {2\times 10 ^ 6} q ≤ 2 × 1 0 6
解法
如果用例 1 一样的方法求解,复杂度 O ( q n ) O(q\sqrt n) O ( q n ) O ( q log n ) O(q \log n) O ( q log n )
事实上,我们只需要找出区间长度 r − l + 1 r-l+1 r − l + 1 a n s = r − l + 1 ans=r-l+1 an s = r − l + 1 p p p a n s p \dfrac{ans}{p} p an s
解释一下:对于目前的循环节长度 ans,如果能找到一个整数,使 ans/x 仍是一个循环节的长度,那么 ans/x 就是一个更小的循环节。我们目标就是对 ans 不断地除,直到除到没有数可以除。我们只要对 r − l + 1 r-l+1 r − l + 1
这份代码略卡了一点常。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #include <bits/stdc++.h> using namespace std;using ll=long long ;int read () int f=1 ,x=0 ;char c=getchar ();while (!isdigit (c)){if (c=='-' )f=-1 ;c=getchar ();}while (isdigit (c)){x=x*10 +c-'0' ;c=getchar ();}return x*f;template <class T >void write (T x) if (x<0 )putchar ('-' ),x=-x;if (x>9 )write (x/10 );putchar (x%10 +'0' );const int N = 1e6 +5 ;char s[N];const int b=123 ,M=1e9 +7 ;int power_b[N],h[N];int get_hash (int l,int r) if (l==0 )return h[r];return ((h[r]-(ll)h[l-1 ]*power_b[r-l+1 ])%M+M)%M;int p[N],v[N],m;void sieve () for (int i=2 ;i<N;i++){if (v[i]==0 ){for (int j=0 ;j<m;j++){if (p[j]>v[i] || p[j]*i>=N)break ;int main () sieve ();1 ]=b;for (int i=2 ;i<N;i++) power_b[i]=(ll)power_b[i-1 ]*b%M;int n,q;scanf ("%d%s%d" ,&n,s,&q);0 ]=s[0 ];for (int i=1 ;i<n;i++)h[i]=((ll)h[i-1 ]*b+s[i])%M;while (q--){int l=read ()-1 ,r=read ()-1 ;int ans = r-l+1 ;int x=r-l+1 ;while (x!=1 ){int k = (ans)/v[x];if (get_hash (l,r-k) == get_hash (l+k,r))ans/=v[x];write (ans);putchar ('\n' );return 0 ;
Beads
LOJ #2427. 「POI2010」珍珠项链 Beads
Byteasar 决定制造一条项链,她买了一串珠子,她有一个机器,能把这条珠子切成很多段,使得每段恰有 k k k k > 0 k>0 k > 0 k k k k k k k k k 1 , 2 , 3 1,2,3 1 , 2 , 3 3 , 2 , 1 3,2,1 3 , 2 , 1
解法
尝试暴力枚举每个 k k k O ( ∑ i = 1 n ⌊ n i ⌋ ) = O ( ∑ i = 1 n n i ) = O ( n ∑ i = 1 n 1 i ) \displaystyle O\left(\sum_{i=1}^{n}\bigg\lfloor\dfrac{n}{i}\bigg\rfloor\right)= O\left(\sum_{i=1}^{n}\dfrac{n}{i}\right) = O\left(n\sum_{i=1}^{n}\dfrac{1}{i}\right) O ( i = 1 ∑ n ⌊ i n ⌋ ) = O ( i = 1 ∑ n i n ) = O ( n i = 1 ∑ n i 1 ) O ( log n ) O(\log n) O ( log n ) O ( n log n ) O(n \log n) O ( n log n )
接下来就是解决反转串的问题。为此,我们可以再增加一个后缀的哈希,同理计算即可。为了判重,可以用哈希表(这里使用 unordered_map),并且我们不需要清除这个哈希表,而是用到一个使时间标记的技巧。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 #include <bits/stdc++.h> using namespace std;using ll=long long ;using ull=unsigned long long ;using pii=pair<int ,int >;#define begend(x) x.begin(),x.end() #define mem0(x) memset(x,0,sizeof(x)) #define YES puts("YES" ) #define NO puts("NO" ) int read () int f=1 ,x=0 ;char c=getchar ();while (!isdigit (c)){if (c=='-' )f=-1 ;c=getchar ();}while (isdigit (c)){x=x*10 +c-'0' ;c=getchar ();}return x*f;const int N = 2e5 +5 ;int n,a[N];const ll b=19260817 ,M=1e9 +9 ;int ans=0 ;int ans_cnt=0 ,ans_k[N];int > vis;ll get_pre (int l,int r) {return ((h_pre[r]-h_pre[l-1 ]*bp[r-l+1 ])%M+M)%M;ll get_suf (int l,int r) {return ((h_suf[l]-h_suf[r+1 ]*bp[r-l+1 ])%M+M)%M;int main () 0 ]=1 ;for (int i=1 ;i<N;i++)bp[i]=bp[i-1 ]*b%M;int n=read ();for (int i=1 ;i<=n;i++)a[i]=read ();for (int i=1 ;i<=n;i++)h_pre[i]=(h_pre[i-1 ]*b+a[i])%M; for (int i=n;i>=1 ;i--)h_suf[i]=(h_suf[i+1 ]*b+a[i])%M; for (int k=1 ;k<=n;k++){if (n/k < ans)break ; int cnt = 0 ; for (int i=1 ;i*k<=n;i++){int hash_pre = get_pre ((i-1 )*k+1 ,i*k);if (vis[hash_pre]==k)continue ; int hash_suf = get_suf ((i-1 )*k+1 ,i*k);if (cnt>ans){ 0 ;if (cnt==ans){printf ("%d %d\n" ,ans,ans_cnt);for (int i=0 ;i<ans_cnt;i++){printf ("%d " ,ans_k[i]);return 0 ;
Antisymmetry
LOJ #2452. 「POI2010」反对称 Antisymmetry
对于一个 0 / 1 0/1 0/1 0 0 0 1 1 1 00001111 00001111 00001111 010101 010101 010101 1001 1001 1001 n n n 0 / 1 0/1 0/1 1 ≤ n ≤ 500 000 1\le n\le 500\ 000 1 ≤ n ≤ 500 000
解法
O ( 1 ) O(1) O ( 1 ) O ( n 2 ) O(n^2) O ( n 2 )
观察到几个性质:
反对称子串的长度是偶数;
若 s [ l . . r ] s[l..r] s [ l .. r ] s [ l + 1.. r − 1 ] s[l+1..r-1] s [ l + 1.. r − 1 ]
因此,可以枚举对称轴,然后二分答案,找到最长可以延伸的范围。复杂度 O ( n log n ) O(n\log n) O ( n log n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <bits/stdc++.h> using namespace std;using ll=long long ;const int N = 5e5 +5 ;char s[N];int n;const ll b=19260817 ,M=1e9 +9 ;bool check (int m,int len) if (len==0 )return 1 ; 2 ])%M+M)%M;1 ]-h2[m+len+1 ]*bp[len*2 ])%M+M)%M;return hash1==hash2;int main () int n;scanf ("%d%s" ,&n,s+1 );0 ]=1 ;for (int i=1 ;i<N;i++)bp[i]=bp[i-1 ]*b%M;for (int i=1 ;i<=n;i++)h1[i]=(h1[i-1 ]*b+(s[i]-'0' ))%M;for (int i=n;i>=1 ;i--)h2[i]=(h2[i+1 ]*b+((s[i]-'0' )^1 ))%M; 0 ;for (int k=1 ;k<=n;k++){int l=0 ,r=min (k,n-k);while (l<r){int mid = (l+r+1 )>>1 ;if (check (k,mid))l=mid;else r=mid-1 ;printf ("%lld\n" ,ans);return 0 ;