经典的区间三个贪心问题。再总结一下，以作复习。

选择不重叠区间

有 nn 个区间 [li,ri][l_i,r_i]，选择尽量多的区间，使得区间之间不重叠（端点可以重叠）。

将右端点从小到大排序（左端点可以随便排序），然后先选择右端点比较小的（不与之前选过的重叠）。

这样的贪心策略是正确的。

考虑如下一个例子。先选择右端点最小的 [1,4][1,4]，然后右端点次大的 [2,5],[3,5][2,5],[3,5] 重叠无法选择，然后是右端点最大的 [4,6][4,6] 可以选择。即最多可以选出两个区间。

假设一开始没有选择右端点最小的，选择了 [2,5][2,5]， 那么 [1,2][1,2] 的部分就被浪费了，还额外占用了 [4,5][4,5] 的空间，所以一定从右端点小的开始选更划算。

区间选点问题

有 nn 个区间 [li,ri][l_i,r_i]，选择尽可能少的点，使得每一个区间内都有点。

事实上，这个问题的答案和选择不重叠区间的答案是一样的。

为什么两个问题的答案相同？

考虑所有最大不重叠区间，至少要选最大不重叠区间数量的点。（这是答案的下界）
然后，我们证明选最大不重叠区间数量的点一定能覆盖所有区间。
如果一个不重叠区间内需要两个点才能把所有区间覆盖，则需要覆盖的两个区间一定是一个不重叠区间更优答案，与最大不重叠区间矛盾，所以一个不重叠区间内只要选一个点就够了。

还有一种解释是将右端点从小到大排序，然后选择区间的最后一个点。（因为选择前面的点一定没有后面的点划算）

比如在这个例子中，区间 [1,4][1,4] 选择点 44，然后 [2,5],[3,5][2,5],[3,5] 已经被覆盖，跳过，区间 [4,6][4,6] 选择 66。所以至少要选两个点。可以发现，答案确实与最大不重叠区间相同。

区间覆盖问题

有 nn 个区间 [li,ri][l_i,r_i]，选择尽可能少的区间，覆盖线段 [s,t][s,t]。

  1. 先按照左端点从小到大排序。记录目前能到的最右端位置 now（一开始为 0）。
  2. 从所有左端点比最右端位置小的区间中（即 a[i].l <= now），选出右端点最大的，直到覆盖完。
  3. 如果在最后找不到一个左端点比最右端位置小的区间，且此时还没有到 tt，则问题无解。

来看一道具体题目。

例题

LOJ#10002. 喷水装置

长 LL 米，宽 WW 米的草坪里装有 nn 个浇灌喷头。每个喷头都装在草坪中心线上（离两边各 W2\dfrac{W}{2} 米）。我们知道每个喷头的位置（离草坪中心线左端的距离），以及它能覆盖到的浇灌范围。请问：如果要同时浇灌整块草坪，最少需要打开多少个喷头？

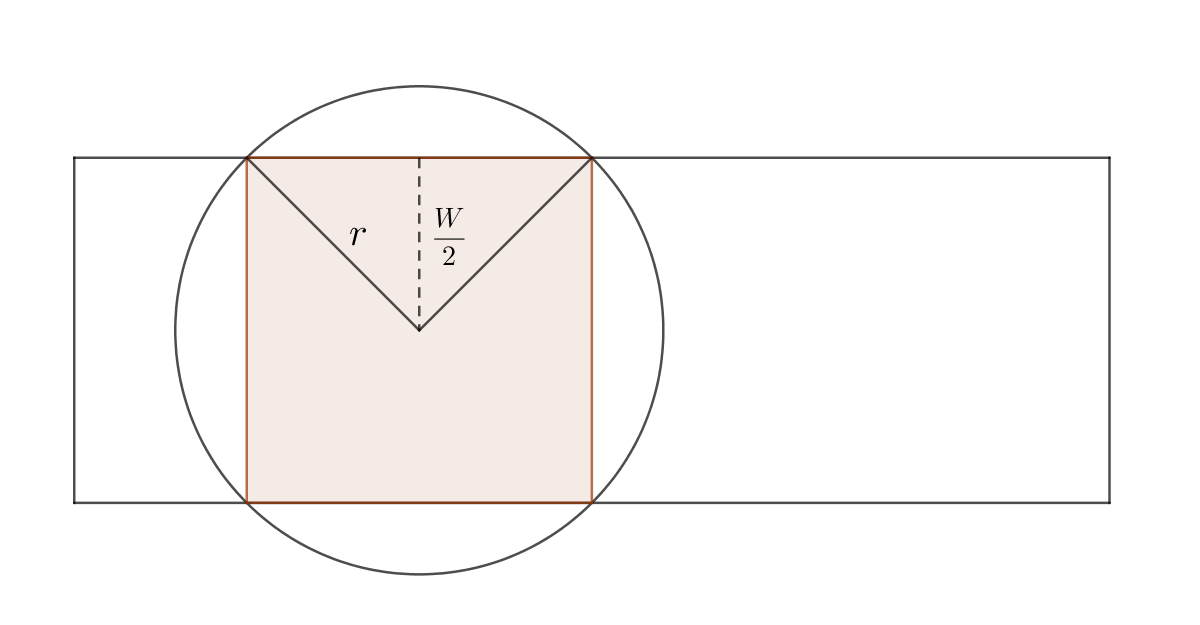
首先，一个喷头的有效区域是一个矩形，可看作一个区间。具体来说，对于一个位置在 dd，半径为 rr 的喷头：

  1. r≤W2r\le\dfrac{W}{2}：此时该喷头无效。
  2. r>W2r>\dfrac{W}{2}：此时该喷头的有效范围为

[d−r2−(W2)2,d+r2−(W2)2]\left[d-\sqrt{r^2-\left(\dfrac{W}{2}\right)^2},d+\sqrt{r^2-\left(\dfrac{W}{2}\right)^2}\right]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;

const int N = 1000;

int n,L,W;

void solve(){
    vector<pair<double,double>> range;

    scanf("%d%d%d",&n,&L,&W);
    for(int i=0;i<n;i++){
        int a,r;
        scanf("%d%d",&a,&r);
        if((double)r<=W/2)continue;
        double h = sqrt(pow(double(r),2)-pow(W/2.,2));
        range.push_back({fmax(0.,a-h),a+h});
    }

    sort(range.begin(),range.end());    

    double now=0; // 现在已经覆盖到的最右位置
    int i=0; // 目前处理到的区间
    int ans = 0; // 选择了几个区间
    while(now<L){ // 还没有覆盖完
        double to=-1;
        // 从所有左端点小于等于覆盖到的最右位置的区间中
        for(;range[i].first<=now&&i<range.size();i++){ 
            to=max(to,range[i].second); // 找到右端点最大值
        }
        if(to==-1){ // 如果没有这样的区间（并且现在还是 now < L 的），则无解
            puts("-1");
            return;
        }
        now = to;
        ans++; // 多一个区间
    }

    printf("%d\n",ans);
    return;
}

int main(){
    int T;scanf("%d",&T);
    while(T--)solve();
}

核心逻辑在第 22~37 行。